Dr. Zulfakriza, S.Si., MT.
Program Studi Teknik Geofisika
Kelompok Keahlian Geofisika Global

Dalam pembahasan kalkulus, kata differensial atau dalam istilah Bahasa Indonesia disebut dengan turunan/diferensiasi merupakan perbandingan perubahan tinggi (selisih tinggi) dan perubahan jarak (selisih jarak). Hal ini terlihat pada persamaan (1), bahwa perbandingan arah y dan arah x dapat didekati dengan pendekatan ax menuju 0 terhadap perbandingan antara selisih perubahan y dan selisih perubahan x.

Persamaan 1

Hampir semua fungsi kontinu dapat dihitung nilai differensialnya secara mudah. Pada pemakaian komputer, permasalahan diferensial merupakan salah satu bagian dari penyelesaian. Dengan kata lain, turunan fungsi dapat didefenisikan sebagai berikut (Persamaan 2)

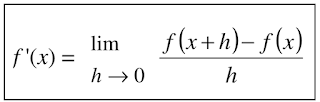
Persamaan 2

Permasalahan fungsi turunan sering dijumpai dalam bidang sains dan rekayasa, salah satunya dalam bidang geofisika. Sementara dalam perhitungan numerik sendiri, turunan fungsi dalam orde yang lebih tinggi, f ‘, f “, f “‘, …, kadang-kadang diperlukan. Misalnya untuk menghitung batas-batas galat interpolasi polinom.

Persoalan turunan numerik ialah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Meskipun metode numerik untuk menghitung turunan fungsi tersedia, tetapi perhitungan turunan sedapat mungkin dihindari. Alasannya, nilai turunan numerik umumnya kurang teliti dibandingkan dengan nilai fungsinya.

Sebagaimana yang telah dijelaskan di atas, bahwa turunan adalah limit dari hasil bagi selisih: yaitu pengurangan dua buah nilai yang besar ( f(x+h) – f(x) ) dan membaginya dengan bilangan yang kecil (h).

Pembagian ini dapat menghasilkan turunan dengan galat yang besar. Selain itu, jika fungsi f dihampiri oleh polinom interpolasi p, selisih nilai fungsi mungkin kecil tetapi turunannya boleh jadi sangat berbeda dengan nilai turunan sejatinya.

Hal ini menjadi mudah dipahami, sebab turunan numerik dapat mendekati kondisi yang sebernarnya. kondisi ini berlawanan dengan integrasi numerik, yang tidak banyak dipengaruhi oleh ketidaktelitian nilai fungsi, karena integrasi pada dasarnya adalah proses untuk mendekati nilai yang sebernarnya.

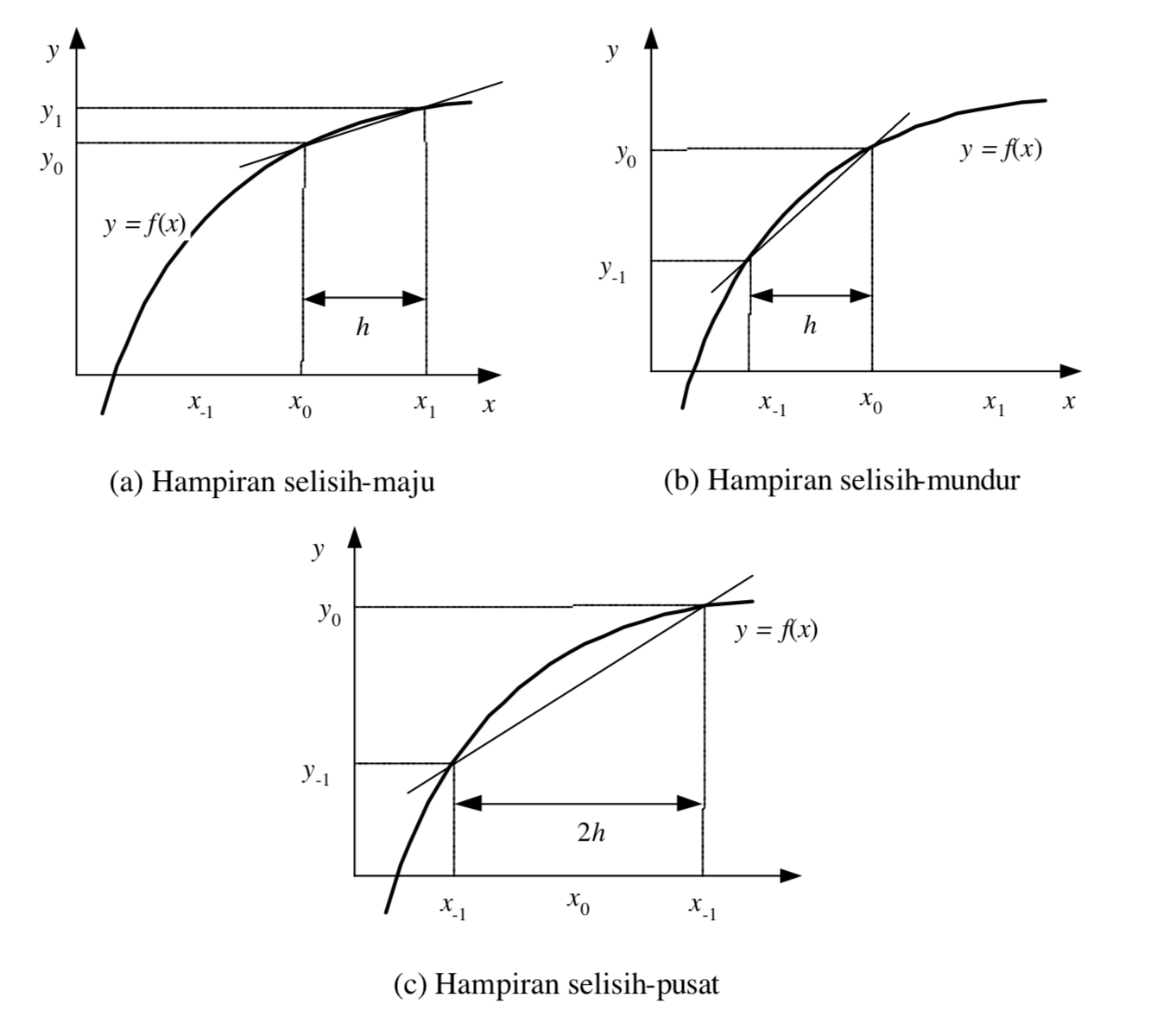
Terdapat tiga pendekatan dalam menghitung nilai f ‘(x0):

1. Hampiran selisih-maju (forward difference approximation)
2. Hampiran selisih-mundur (backward difference approximation)
3. Hampiran selisih-pusat (central difference approximation)

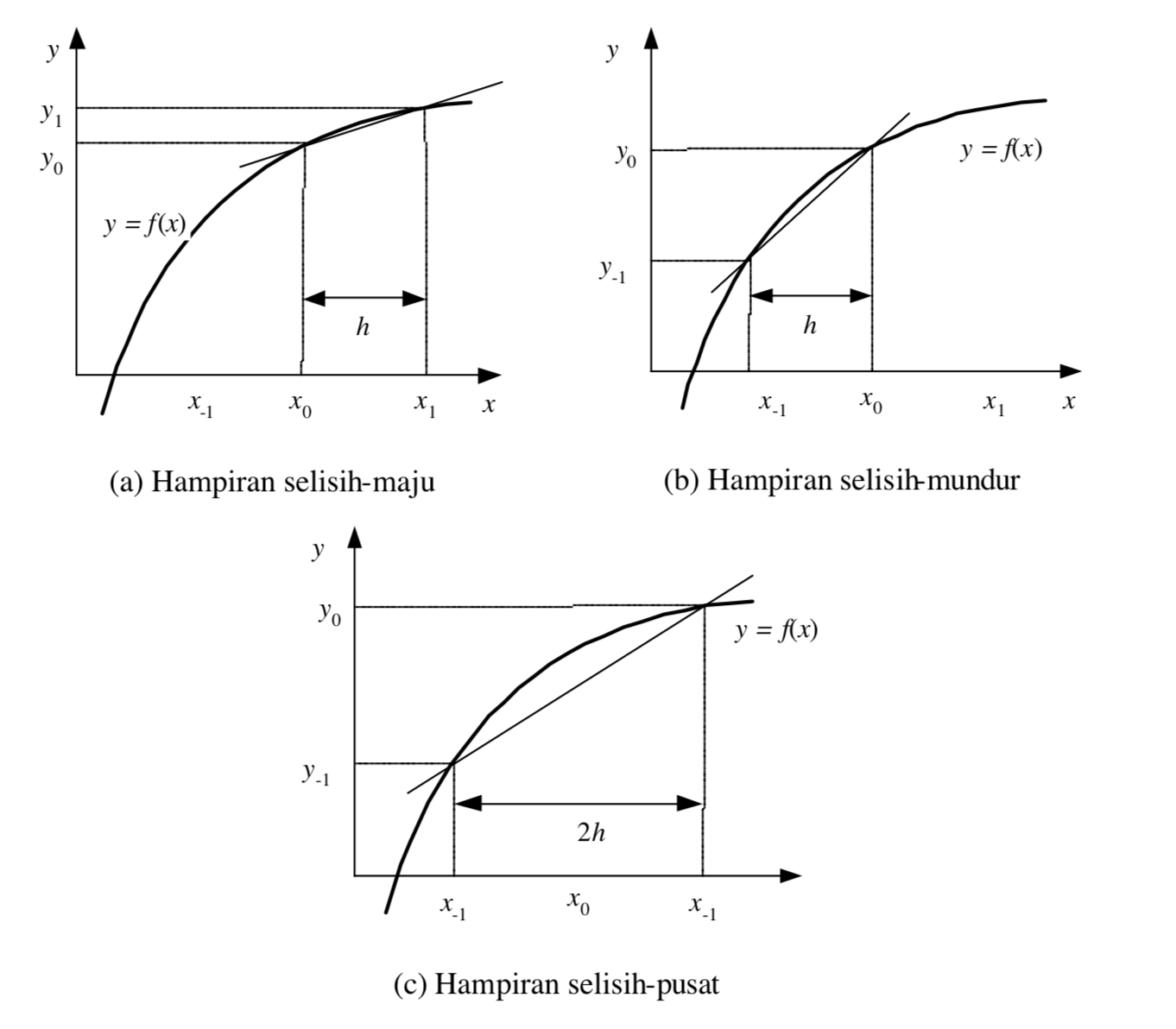
Grafik Fungsi

Silakan unduh bahan kuliah (pdf)

Referensi: Rinaldi Munir, bahan kuliah IF4058 Topik Khusus Informatika I
Sumber: http://www.seisnote.com/2019/10/deferensiasi-numerik-bagian-dari-materi.html